Matching records is one of the most basic data analysis operations. There are many cases where data needs to be aligned across some common value — whether that’s joining between two different tables in a database or across two data sets stored in a file, or matching data sets between two separate entities.
For example, consider two people — Alice and Bob — who each have a list of contacts identified by email addresses and want to know how many connections they have in common. Traditional matching would involve at least one of them sharing all their contacts with the other person to identify matches. This exposes all the contact information regardless of a match and isn’t ideal from a privacy point of view. Privacy-enhancing technologies (PETs) offer a range of solutions for use cases such as this where no personal information is shared with the other party beside the desired output — often leveraging advanced cryptographic techniques. In this blog, we discuss two new cryptographic protocols, Private-ID and PS3I, for variants of this problem, which we refer to as private matching for compute.
The problem of matching records using an identifier while preserving privacy has been well studied as a class of algorithms called private set intersection. However, much of the work in this domain either reveals the matched records to one or both parties or uses a complicated circuit-based construction to preserve privacy. To solve this, we’ve developed Private-ID and PS3I — two new private matching algorithms that can work within real-world constraints, such as when an entire record is unavailable at the time of matching. These algorithms are simpler and, since they do not reveal the matched records, have stronger privacy guarantees than many other existing options. Our own tests demonstrate that because of the inherent parallelizability of these solutions we can execute matching for data sets containing up to 100 million records within an hour.
Private-ID performs an outer join between two databases. It does not reveal any information about the records except for the size of the intersection (how many records overlap). We use elliptic curve cryptography to ensure the privacy of records as we exchange data between two parties. PS3I performs an inner join between two databases and outputs matching records that are encrypted as additive shares. We use elliptic curve cryptography along with Paillier encryption to generate encrypted records that are entered into a multiparty computation framework.
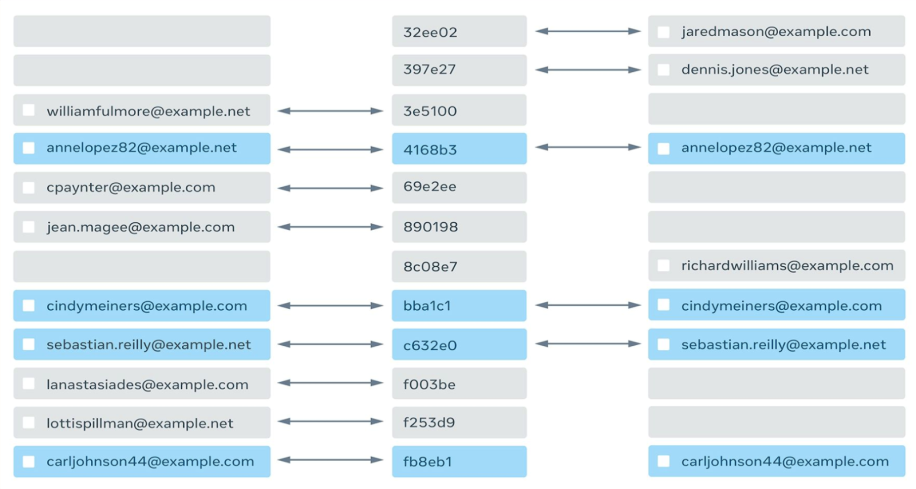
Number of unique attendees via private set intersection
What do we mean by a private set intersection? Let’s walk through an example:
Suppose Alice and Bob both manage a community organization and are jointly planning an event. Both have received RSVPs from attendees. For planning purposes, they want to know the total number of people attending. They are aware that they likely have some overlap, and don’t want to double-count anyone. They also care about the privacy of their attendees’ email addresses, so they cannot directly share their list of emails with each other.
In this example, the private data sets are Alice’s and Bob’s email lists. If Alice and Bob agree to jointly perform a private data analysis, they shouldn’t learn anything about each other’s data sets except for what they agree to compute.
The solution here is an area of research in cryptography called private set intersection (PSI). For example, we can use a special form of encryption wherein double encryption results in the same value, regardless of order.
That is, if we have keyalice and keybob, then:
encryptkeybob(encryptkeyalice(email@address.com)) = encryptkeyalice(encryptkeybob(email@address.com))
We can then apply this directly to our problem:
- First, Alice and Bob encrypt their email addresses and exchange the encrypted values.
- Next, Alice and Bob again encrypt the new values, shuffle them (so they can’t be linked back to the original row), and share back.
- Once shared back, both Alice and Bob can see how many elements are the same. In this example, they can calculate that there are 12 unique email addresses among the total 16 addresses. However, neither Alice nor Bob learns which four email addresses they had in common.
Beyond private set intersection
The previous example performed a very simple analysis on a joined data set: a count of distinct items. It is often the case that we want to do something more complex, but we still want to rely on data from both Alice and Bob. More sophisticated PETs like multiparty computation (MPC) and homomorphic encryption (HE) allow Alice and Bob to perform various downstream computations on larger data sets while keeping everything except the final outcome of the computation protected. Consider the following examples:
- Calculate the total money donated to different categories, where Alice knows the donation amounts and Bob knows people’s category preferences.
- Calculate the test statistics of a randomized control trial, comparing an outcome where the test outcomes are known to Alice and the treatment and control group memberships are known to Bob.
- Train a machine learning (ML) model that estimates lifetime donations, where historical donations are known by Alice and the predictive features (e.g., years active and total events volunteered) are known by Bob.
In each of these examples, Alice and Bob know some information, such as money donated or attendance history, which must remain private. In order to perform these complex analyses as a private computation, the data from Alice and Bob must somehow be joined.
The following presents what would happen in each of these three examples without a PET (i.e., if Alice, Bob, or someone else had access to the full data set).
Example 1: Money by category
Calculate the total money donated to different categories, where Alice knows the donation amounts and Bob knows people’s category preferences.

Result:
Food: $130; Community: $70; Uncategorized: $340
Example 2: Randomized controlled trials
Calculate the test statistics of a randomized control trial, comparing an outcome where the test outcomes are known to Alice and the treatment and control group memberships are known to Bob.

Result:
Treatment: 1 Attend; 1 Did Not Attend
Control: 1 Attend; 1 Did Not Attend
Example 3: Machine learning training
Train a machine learning (ML) model that estimates lifetime donations, where historical donations are known by Alice and the predictive features (e.g., years active and total events volunteered) are known by Bob.

Result:
Regression model with lifetime donations as the dependent variable; years active and total events volunteered as independent variables.
Private matching for compute
In all the examples above, we assumed that we had a full view of the data. This allowed us to calculate the appropriate result but also to align the data. As it turns out, attempting to align the data within a PET, such as an MPC, is a difficult problem. In fact, it’s hard enough that it makes the whole process computationally expensive.
Instead, we extend the ideas of PSI — leveraging the double encryption mechanism — to create two new ways to perform this data joining: Private-ID and PS3I. These allow Alice and Bob to feed encrypted data into an MPC or other PET in a way that’s already aligned.
Privacy requirements:
- Neither party learns anything about the other party’s data set except for the final outcome of computation (e.g., the trained model or the final aggregated statistic).
- Neither party learns which one of its records was in the intersection and which one was not. The only thing the parties learn is the total number of matched records.
Application requirements:
- Only the identifier is needed for the join, and features can be added to records even after the join is done.
- We would like to be able to perform multiple downstream computations without having to repeat the private matching component.
- One party can have a database that is static, while another party can stream its database as batches.
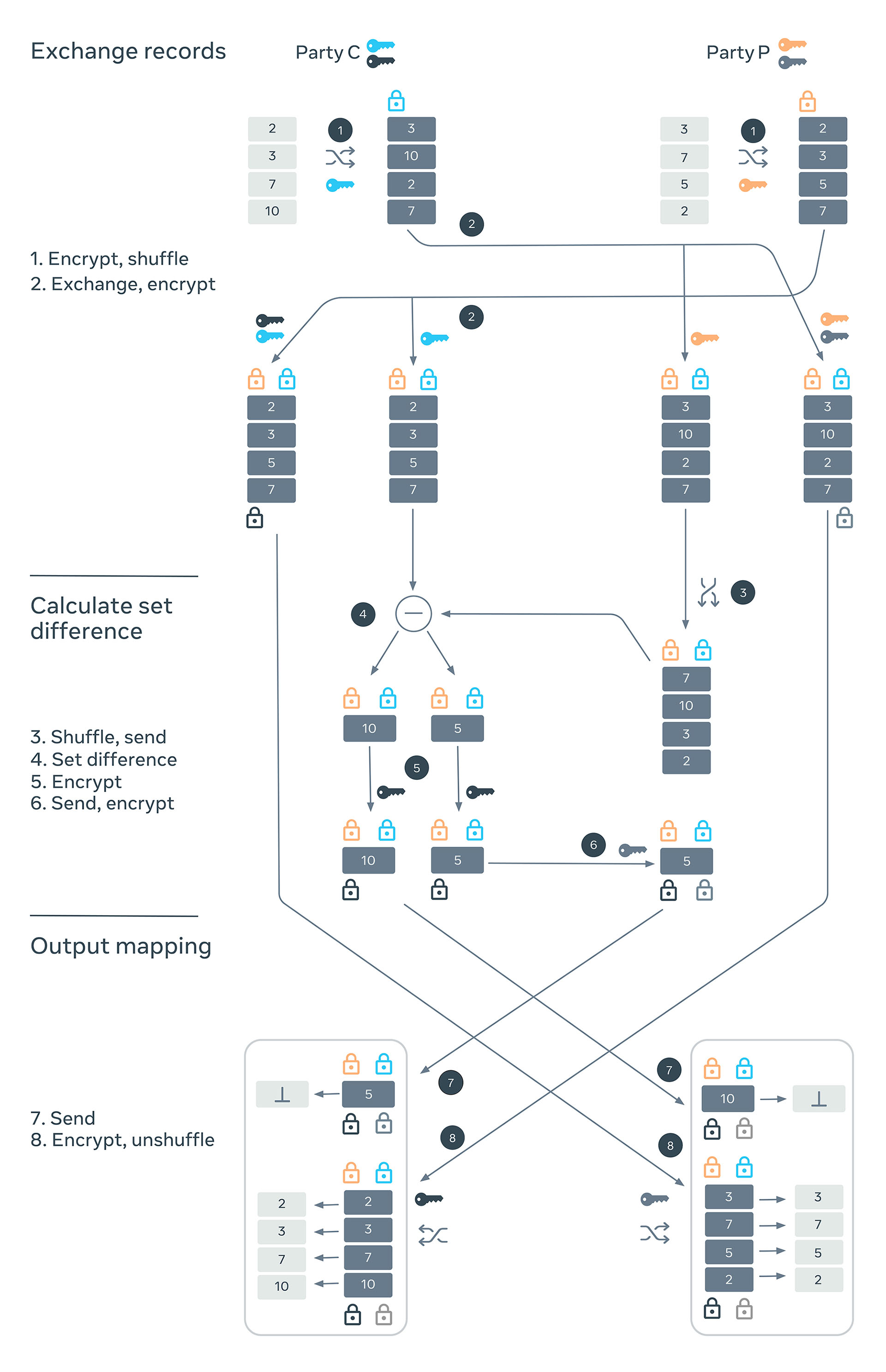
Private-ID
In the Private-ID formulation, the two parties want to generate a single set of keys for all the records without revealing the records themselves, to generate something like:
An interesting thing to note about this ID spine in the middle that connects the records in two databases: Neither party knows whether its record matched with the other party’s, but if it did, the records would have the same ID.
The three stages of the Private-ID algorithm are:
- Encrypt and exchange records: Two parties, C and P, generate two sets of secret keys each, which they will use to encrypt the records as points on an elliptic curve. They shuffle and encrypt with one of their keys and send it to the other party. Each party then creates two copies of the encrypted records it has received from the other party. It encrypts one of them with one of its keys and another with both of its keys. Thus, one set of records is encrypted with two keys and another with three.
- Calculate set difference: The records that are encrypted with two keys can be used to calculate a symmetric set difference. Party P sends its doubly encrypted records to party C after shuffling. Party C calculates a symmetric set difference, which would allow each party to get identifiers for records that it doesn’t have.
One thing to note here is that if the keys were not shuffled before sending the party P can deduce the matched records. However, the shuffling also breaks the correspondence between the encrypted records and their unencrypted counterparts. This is restored by the versions of the records that are encrypted thrice in the previous step. - Generate mapping from ID to records: The parties can now generate the ID spine by exchanging the records that have been encrypted with all four keys, undoing their shuffling and then appending them to the records generated from the symmetric set difference.
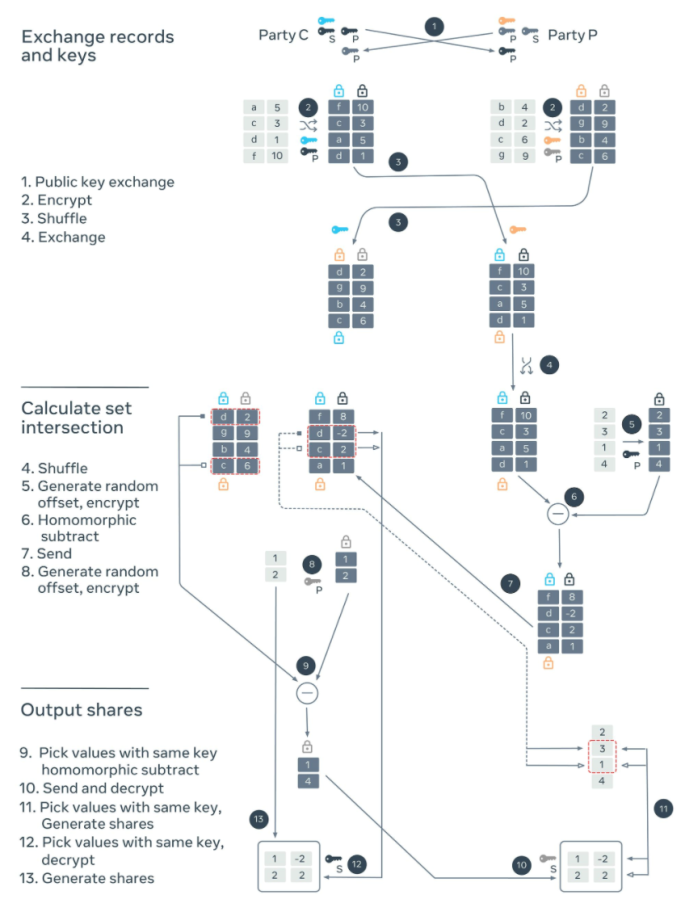
PS3I
The PS3I algorithm also has three stages but uses both elliptic curves and Paillier encryption. Elliptic curves are used for the identifiers on which matching happens. Paillier encryption is used for the values for which additive shares are generated. In this case, a record has both identifiers and values.
- Encrypt and exchange records and keys: The parties C and P generate secret keys for elliptic curves and generate a pair of private and public keys for Paillier encryption. Each party encrypts its records, shuffles, and sends them to the other party. The parties also exchange the public keys for Paillier encryption. On receiving these records, each party encrypts the identifiers with its own secret key. These doubly encrypted identifiers can then be used to match the records.
- Calculate set intersection: Party P shuffles the records it received and encrypts the identifier with its own secret key. It chooses random numbers and homomorphically subtracts them from the values using party C’s public key. These random numbers are one of the additive shares for party C’s value. It then sends the doubly encrypted identifiers and corresponding values to the party C, who can now match the records using double encrypted identifiers. For the records that matched, it also homomorphically subtracts a random number using the party P’s public key. Symmetrically these random numbers are one of the additive shares for party P’s values.
- Output shares: Party C decrypts the values it got from the party P to get its share for its value. It sends the encrypted values to the party P along with the indices that matched. Party P decrypts these encrypted values to get its shares of its values. It uses the indices to choose the random numbers it had generated to get the share for party C’s values.
Open source and future directions
We implemented these protocols in Rust and are open-sourcing them today at https://github.com/facebookresearch/Private-ID. We chose Rust for its superior safety features and ease of writing multithreaded code. We use Curve 22519 from the Dalek library as our elliptic curve and the Paillier implementation from rust-paillier crate. We have tested our implementations on inputs with many records, where Private-ID can generate IDs for 100 million records in 60 minutes and PS3I can generate additive shares for 5 million records in the same amount of time.
Our hope is that this type of technology can help reduce data collection over time. We are open-sourcing our implementation as a first step to enable building learning pipelines that are encrypted end-to-end. There is still a lot of work to do before this can be applied to any of our products, but we are continuing to make progress in this area.