Maintaining scalability and infrastructure reliability are important considerations for any large-scale network. Ensuring consistency when propagating updates across a large network of peers is a problem that has been extensively studied, but enforcing the integrity of those updates is a separate challenge. Traditional methods for update integrity can introduce compromises with respect to efficiency and scalability. To address these concerns, we’ve employed homomorphic hashing, a cryptographic primitive that has been used in other applications, including efficient file distribution and memory integrity checking.
We have implemented LtHash, a specific homomorphic hashing algorithm, within the update propagation step of our Location Aware Distribution configuration management system. Today we are releasing the implementation we use in Folly, our open source C++ library. For more information about this work, see our paper.
The challenges of securing update propagation at scale
In a distributed system, database replication involves copying information to keep it synchronized across multiple locations to improve availability and read latency. Database modifications must be propagated to each location to maintain the consistency of the replicated objects with the master database. For a model in which database writes are published by a central distributor that manages the master database, the distributor is responsible for propagating updates to a set of subscribers in a reliable and efficient manner. The simplest way to achieve this is for the distributor to be in charge of directly sending the updates to each subscribed client.
In practice, however, this does not scale well, as the number of subscribed clients and the rate of updates increases. Handling frequent updates with a centralized distributor can saturate the network interface controller, leaving it unable to finish distributing one update before the next one is ready to be pushed. A more efficient way to offload the responsibility of the distributor propagating the changes is to delegate the propagation through its clients. In other words, some subscribers can participate in forwarding the distributor’s original updates to other subscribers.
This approach effectively reduces the number of connections the distributor must manage, without incurring an unnecessary bandwidth overhead. But now, to ensure consistency, each downstream subscriber needs to trust a set of intermediate subscribers to have correctly propagated the original updates. The challenge of maintaining the integrity of the distributor’s updates across a network of subscribers that could alter those updates is what we refer to as the secure update propagation problem.
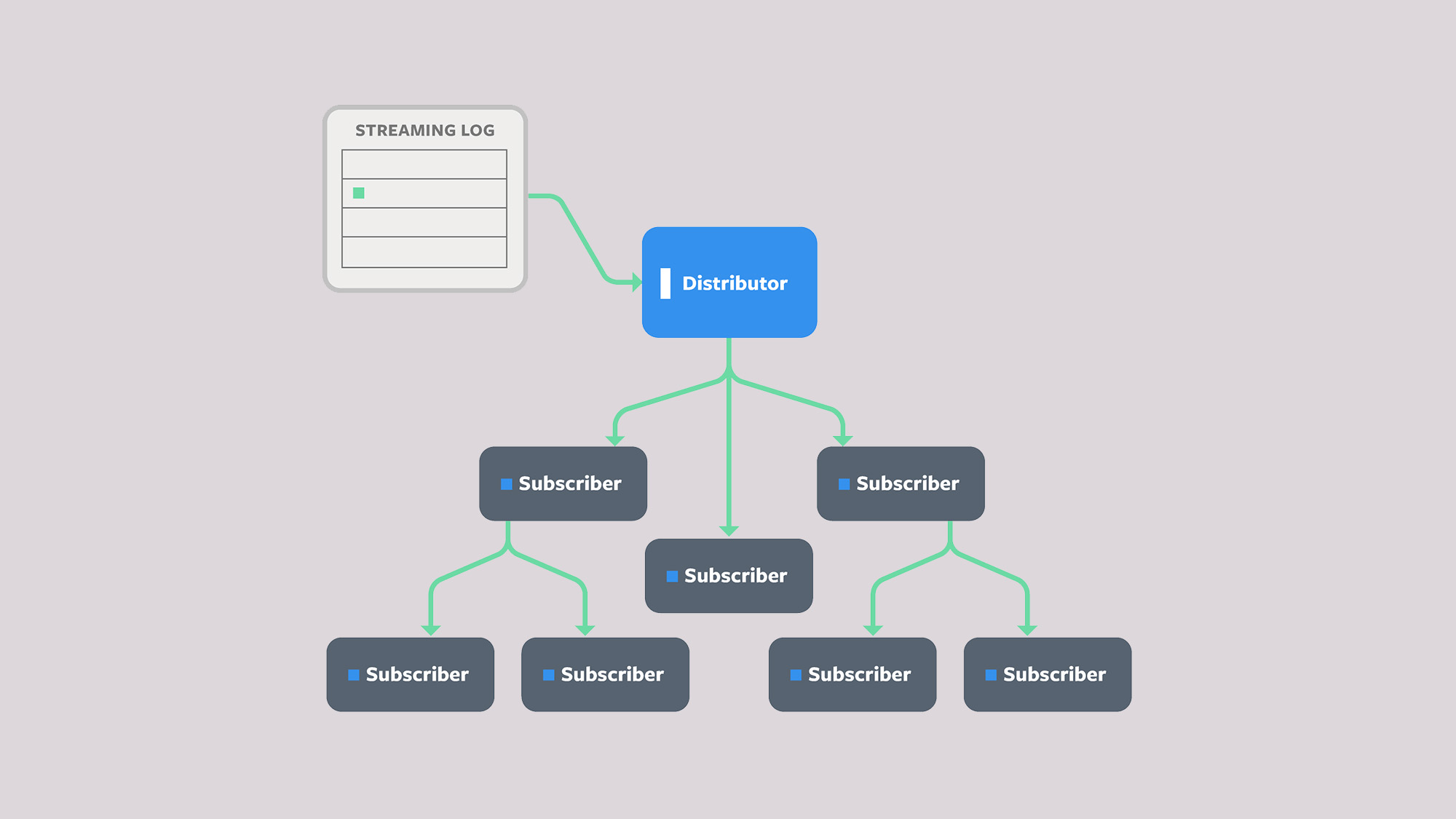
To address this problem, the distributor can use digital signatures to assert the authenticity and integrity of the messages it distributes. Concretely, the distributor generates a public and private key pair, publishes the public key to every subscriber upon joining the network, and keeps the private key secret. The per-update signatures can then be constructed over either the contents of the update or the contents of the updated database. Each of these approaches offers various efficiency trade-offs, outlined below.
Signing each update. The most straightforward approach to handling update propagation securely is for the distributor to directly sign the contents of each update that gets sent to its subscribers. Subscribers can then use the update’s signature to verify the update contents before applying it to their database replica. While this approach successfully prevents an attacker from modifying updates maliciously, it also adds complications to the handling of batch updates and offline database validation:
- Batch updates. When one subscriber needs to update another with a sequence of updates, the signatures for each of these updates must be sent and verified individually by the recipient. This situation can arise if a subscriber has been disconnected from the network for some period of time and then attempts to rejoin and receive the latest updates. Having signatures on each update means that if the subscriber missed m updates, it must now verify m signatures in order to catch up.
- Offline database validation. In offline validation, a subscriber wishes to validate its database replica against the original copy held by the distributor, without having to reach out to the distributor. The subscriber performs this validation by scanning the entire database to perform an integrity check. With an approach in which each update is signed, the subscriber must validate a signature for every update it has received since the original version of the database.
Typically in these scenarios, it would be more efficient for the subscriber to directly ask the distributor to send and re-sign an updated database. But within a large system where network failures are more common, this approach quickly devolves and a large number of subscribers must keep reaching out to the distributor for updates, defeating the purpose of delegating the propagation responsibilities in the first place.
Signing the database. An alternative approach is to rely on a signature algorithm computed over the database contents after each update, rather than on the update itself. When each subscriber receives the update (with the database signature), they can apply the update and then use the signature to verify that the updated database is still valid.
Now, when handling batch updates and offline validation, subscribers can apply updates to their database replicas without having to worry about integrity. Once they reach the final result, they can perform a single integrity check to verify that their end state matches the distributor’s end state. In this scenario, each batch operation requires only a single signature validation as opposed to one for each update. However, the main drawback to directly signing the database in this manner is that for each update published, the distributor must iterate over the entire database to produce the signature. Similarly, each subscriber must load the entire database into memory in order to verify the database signature. In practice, this approach does not scale well with data size or update rate, and is likely to be impractical in many real-world applications.
Efficiently updatable hashing. Ideally, we want to take an approach that provides integrity of updates using a computation that does not depend on the size of the database or total number of updates. To address these issues, the distributor can use an efficiently updatable collision-resistant hash function to hash the entire database into a small digest. The resulting digest would be directly signed, as opposed to having the distributor sign the database itself. This guarantees that on each update, the “efficiently updatable” property of the hash function allows the distributor to compute the hash of the updated database using only the hash of the previous database version and the update. The collision-resistant property of the hash function, along with the unforgeability of the signature algorithm, ensures integrity through the sequence of updates.
Merkle trees provide a partial solution to this problem. Associating each database row with a leaf node of the tree and signing the root hash using the distributor’s signing key allows the distributor to update the database signature in time proportional to the depth of the Merkle tree (i.e., logarithmic in the database size). However, this improved update and verification performance can be attained only by subscribers who keep a representation of the entire Merkle tree in memory — thus requiring memory overhead linear in the number of database rows.
A truly efficient solution would allow the distributor and its subscribers to update the database hash entirely independent of the size of the database. These requirements are satisfiable through the use of homomorphic hashing.
Implementing homomorphic hashing with LtHash
Intuitively, homomorphic hashing answers the question, “Given the hash of an input, along with a small update to that input, how can we compute the hash of the new input (with the update applied) without having to recompute the entire hash from scratch?” We use LtHash, a specific homomorphic hashing algorithm based on lattice cryptography, to create an efficiently updatable checksum of a database. This checksum, along with a signature from the distributor of the database, allows a subscriber to validate the integrity of database updates. We chose LtHash in favor of other homomorphic hashing algorithms for its performance and straightforward implementation.
LtHash takes a set of arbitrarily long elements as input, and produces a 2KB hash value as output. Two LtHash outputs can be “added” by breaking up each output into 16-bit chunks and performing component-wise vector addition modulo 216.
LtHash has the following two properties:
- Set homomorphism: For any two disjoint sets S and T, LtHash(S) + LtHash(T) = LtHash(S ∪ T).
- Collision resistance: It is difficult (computationally infeasible) to find two distinct sets S and T for which LtHash(S) = LtHash(T).
How is LtHash relevant to update propagation? Suppose we have a database D consisting of three indexed rows:
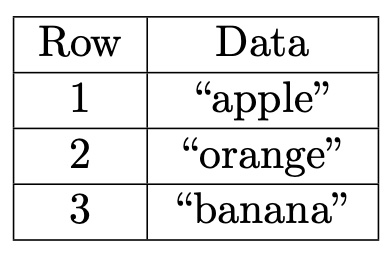
The database hash would be computed as the sum of the hashes of each row along with the row index:
LtHash(D) = LtHash(<1, "apple">) + LtHash(<2, "orange">) + LtHash(<3, "banana">)
Now, suppose an update comes along that changes row 2 from “orange” to “peach”, and let D* represent the updated database. Instead of having to recompute LtHash (D*) from scratch, we can use the existing hash LtHash (D) to get:
LtHash(D*) = LtHash(D) + LtHash(<2, "peach">) - LtHash(<2, "orange">)
By the set homomorphism property of LtHash, the output is guaranteed to be consistent with the result of directly computing LtHash on the updated database.
In update propagation, the distributor and its subscribers can use LtHash to efficiently modify the database hash on each update. Then, the distributor can sign this hash, so that when the subscriber receives this signature, they can apply the same transformations on the hash outputs to reconstruct the database hash, and then validate that it matches the distributor’s signature. The advantage to performing the validation of updates in this way is that we can recompute the hash of an updated database using only the output hash of the existing database and its update. In particular, we don’t need to iterate over every entry of the database to compute the hash.
We have deployed LtHash within the update propagation step of Facebook’s Location Aware Distribution configuration management system. We are now exploring other applications within Facebook’s infrastructure, and have made the LtHash implementation available in Folly in hopes that we can renew attention to homomorphic hashing from the academic community and industry alike.
Special thanks go to Steve Weis, David Freeman, Soner Terek, Ali Zaveri, and the rest of the team for their help in formalizing the problem and in the reviewing of our proposed solutions.