- Facebook is open-sourcing FBGEMM, a high-performance kernel library, optimized for server-side inference.
- Unlike other commonly available libraries, FBGEMM offers optimized on-CPU performance for reduced precision calculations used to accelerate deep learning models.
- The library has been deployed at Facebook, where it’s delivered greater than 2x performance gains with respect to our current production baseline.
- FBGEMM offers high performance on native tensor formats (unlike many other libraries that require repacking tensors for best performance).
- It offers substantial plug-and-play functionality and performance by generating high-performance shape- and size-specific kernels at runtime.
To enable large-scale production servers to run the newest, most powerful deep learning models efficiently, we have created FBGEMM, a low-precision, high-performance matrix-matrix multiplications and convolution library. FBGEMM is optimized for server-side inference, and unlike previously available alternatives, it delivers both accuracy and efficiency when performing quantized inference using contemporary deep learning frameworks. With this library, we have achieved greater than 2x performance gains on the current generation of CPUs with respect to our current production baseline.
We are now open-sourcing FBGEMM to provide other engineers with all the fundamental building blocks for performing efficient low-precision inference, packaged in a convenient single library. You can deploy it now using the Caffe2 front end, and it will soon be callable directly by PyTorch 1.0 Python front end.
Together with QNNPACK, a new library for mobile devices that we open-sourced last week, engineers now have comprehensive support for quantized inference as part of the PyTorch 1.0 platform.
FBGEMM offers several key features:
- It is specifically optimized for low-precision data, unlike the conventional linear algebra libraries used in scientific computing (which work with FP32 or FP64 precision).
- It provides efficient low-precision general matrix-matrix multiplication (GEMM) for small batch sizes and support for accuracy-loss-minimizing techniques such as row-wise quantization and outlier-aware quantization.
- It also exploits fusion opportunities to overcome the unique challenges of matrix multiplication at lower precision with bandwidth-bound pre- and post-GEMM operations.
FBGEMM has been deployed at scale here at Facebook, where it has benefited many AI services, end to end, including speeding up English-to-Spanish translations by 1.3x, reducing DRAM bandwidth usage in our recommendation system used in feeds by 40%, and speeding up character detection by 2.4x in Rosetta, our machine learning system for understanding text in images and videos. Rosetta is used by many teams across Facebook and Instagram for a wide variety of use cases, including automatically identifying content that violates our policies, more accurately classifying photos, and surfacing more-personalized content for people using our products.
Why GEMM efficiency matters
Fully connected (FC) operators are the biggest consumers of floating point operations (FLOPs) in the deep learning models deployed in Facebook’s data centers. We performed data-center-wide profiling for FLOPs usage in representative models running in production here at Facebook. The pie chart below shows the distribution of the deep learning inference FLOPs in our data centers measured over a 24-hour period.

FC operators are just plain GEMM, so overall efficiency directly depends on GEMM efficiency. Many deep learning frameworks implement convolution as im2col followed by GEMM, because performant GEMM implementations are readily available in linear algebra libraries from the high-performance computing (HPC) domain. But straightforward im2col adds overhead from the copy and replication of input data, so some deep learning libraries also implement direct (im2col-free) convolution for improved efficiency. As explained in more detail below, we provide a way to fuse im2col with the main GEMM kernel to minimize im2col overhead. The high-performance GEMM kernel is a critical part, but it’s not the only one. In general, there is a mismatch between what HPC libraries provide and the requirements of deep learning inference. HPC libraries usually do not support quantized GEMM-related operations efficiently. They are not optimized for shapes and sizes of matrices common in deep learning inference. And they do not take advantage of the constant nature of the weight matrix.
Deep learning models have typically used FP32 data types for representing activations and weights, but computations with mixed-precision data types (8-bit or 16-bit integers, FP16, etc.) are generally much more efficient. Recent industry and research works have shown that inference using mixed-precision works well without adversely affecting accuracy. FBGEMM uses this alternative strategy and improves inference performance with quantized models. Furthermore, newer generations of GPUs, CPUs, and specialized tensor processors natively support lower-precision compute primitives, such as FP16/INT8 in Nvidia tensor cores or INT8 in Google processors. So the deep learning community is moving toward low-precision models. This movement indicates that quantized inference is a step in the right direction, and FBGEMM provides a way to perform efficient quantized inference on current and upcoming generation of CPUs.
Understanding low-precision inference
Implementing high-accuracy, low-precision inference is essential for optimizing deep learning models. In developing FBGEMM, we used a quantization strategy similar to the one described in detail in this paper. Each value in a matrix is quantized with the help of a scale factor and a zero point in an affine way, so computations in the quantized domain map directly to computations in real domain. These scale- and zero-point values are shared among multiple entries in the matrix (e.g., all rows may have the same scale and zero point). In the equation below, A is the real-valued matrix, and Aq is the quantized matrix; a_scale is a real-valued constant, and a_zero_point is a constant in quantized domain.
![]()
With this quantization framework, we can represent matrix-matrix multiplications in the quantized domain as follows:
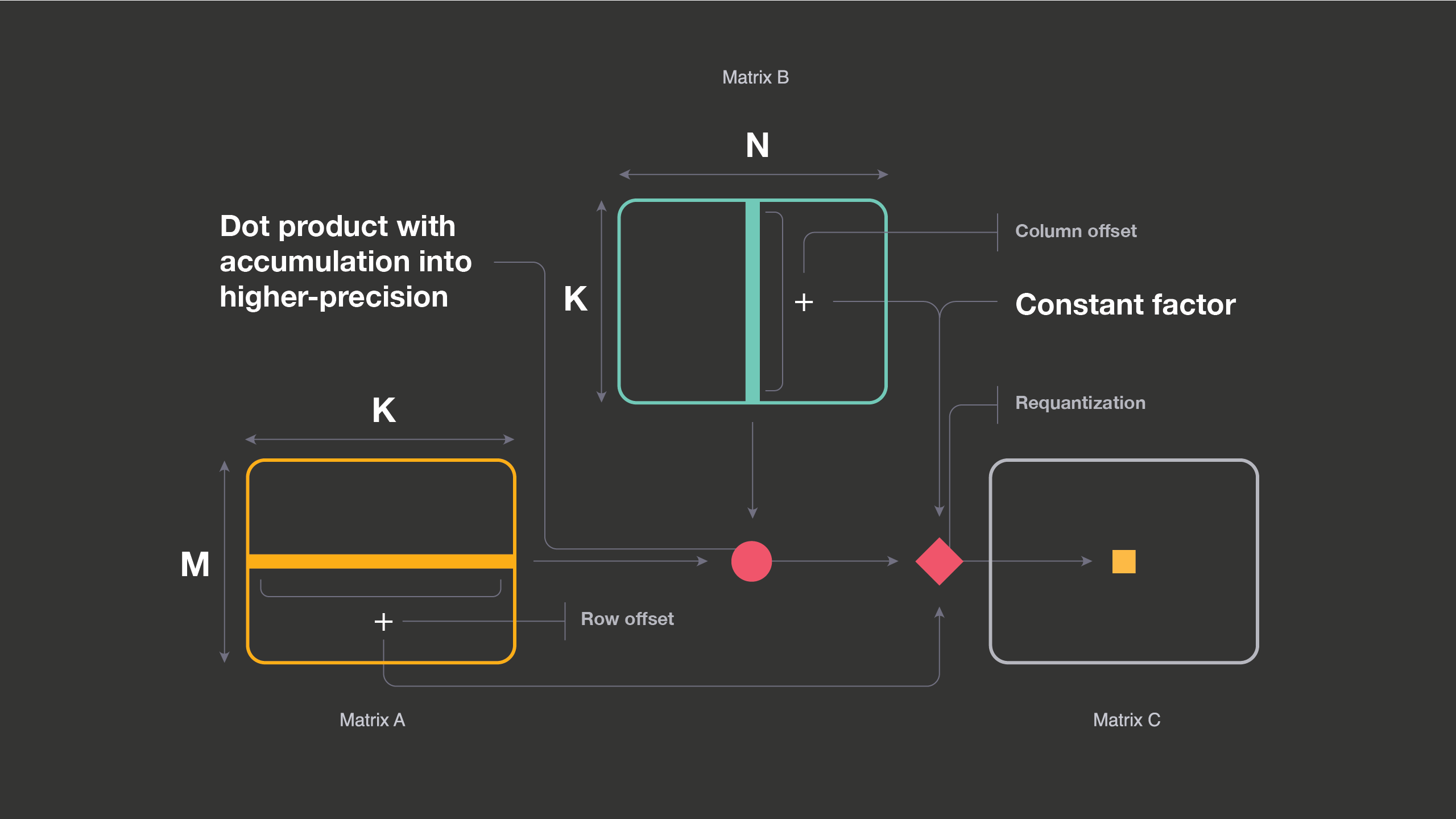 It is important to note several details:
It is important to note several details:
1) Each output value (i, j) in the C matrix requires the sum of ith row of A matrix (row offset), the sum of jth column of B matrix (column offset), and a constant factor in addition to the dot product.
2) If one of the matrices is constant, the constant factor computations can be combined with row (or column) offsets calculations for that matrix. These offsets are used later during the requantization step.
3) Dot product results are accumulated into higher precision and are scaled back to lower precision for the next layer. We call this process requantization.
These background details highlight that when we perform low-precision GEMM, there are other operations around it that are equally important for overall efficiency. If these extra operations (such as row offset calculation or post-accumulation quantization) are not performed carefully along with low-precision GEMM, they can offset the gains of working at lower precision.
Deep dive on FBGEMM’s key features
FBGEMM is distinct from other libraries in several ways: It combines small compute with bandwidth-bound operations. It exploits cache locality by fusing post-GEMM operations with macro kernel and provides support for accuracy-loss-reducing operations. And it supplies modular building blocks to construct an overall GEMM pipeline as needed by plugging and playing different front-end and back-end components.
A key ingredient of FBGEMM is performant low-precision GEMM, which we have implemented using an approach similar to the one taken by other research works (Goto et al. and BLIS framework) targeting FP32 and FP64 data types but not low-precision. The following sample code shows a typical way of implementing high-performance GEMM on modern CPU architectures. Here M, N, and K are standard matrix dimensions: A is an MxK matrix, B is a KxN matrix, and C is an MxN matrix. MCB, NCB, KCB, MR, and NR are target-specific constants, and their values depend on available caches and registers on a given CPU. (CB refers to cache block and R refers to register.) The naive three-loop matrix-matrix multiplication is converted into the following five loops around a microkernel for an implementation that works well with a CPU memory hierarchy with multilevel caches and vector registers.
Loop1 for ic = 0 to M-1 in steps of MCB
Loop2 for kc = 0 to K-1 in steps of KCB
//Pack MCBxKCB block of A
Loop3 for jc = 0 to N-1 in steps of NCB
//Pack KCBxNCB block of B
//--------------------Macro Kernel------------
Loop4 for ir = 0 to MCB-1 in steps of MR
Loop5 for jr = 0 to NCB-1 in steps of NR
//--------------------Micro Kernel------------
Loop6 for k = 0 to KCB-1 in steps of 1
//update MRxNR block of C matrix
As shown in this example, high-performance GEMM implementations work by packing currently used blocks of A and B matrices into smaller chunks that are accessed sequentially in the innermost microkernel. “Packing” here refers to reorganization of matrix data into another array such that the access pattern in the inner kernel of the optimized implementation is sequential. Sequential access of data in the inner kernel is important for achieving high effective bandwidth on modern hardware architectures. Packing is a bandwidth-bound operation because it only reads and writes data. So if we can combine small compute operation with the bandwidth-bound packing operation, the compute cost gets overlapped, and overall packing time remains the same.
We take advantage of the bandwidth-bound nature of packing routines and combine simple compute operations with packing. The figure below shows various packing routines that we have implemented so far. For example, PackingWithRowOffset performs row offset calculations while reorganizing the data in the necessary format for the inner kernel. The row offsets are calculated only for the block that is currently getting packed, i.e., the MCBxKCB block. These row offsets are used later in the post-GEMM requantization pipeline. The advantage of calculating row offsets while packing is that we do not need to make two passes over the A matrix data, thereby avoiding moving data multiple times to the CPU and also avoiding cache pollution. Newer packing routines can also be added while reusing the rest of the flow.
It’s important to note that one of the matrices in GEMM for inference is the weight matrix and is constant during inference. We can therefore prepack it once and use it multiple times for different activations, avoiding the cost of repacking (shown inside Loop3 in the code above). The relative cost of packing the weight matrix can be significant if the activation matrix is small. But this cost must be paid by general GEMM implementations not specifically designed for the case when one of the matrices is constant.
FBGEMM is designed from the ground up while keeping these requirements in mind. It allows us to use prepacked matrices, which avoids large internal memory allocations and allows fusion of post GEMM operations such as nonlinearities, bias addition, and requantization. The FBGEMM library targets quantizations to 8-bit integers because our target hardware efficiently supports 8-bit integer operations.
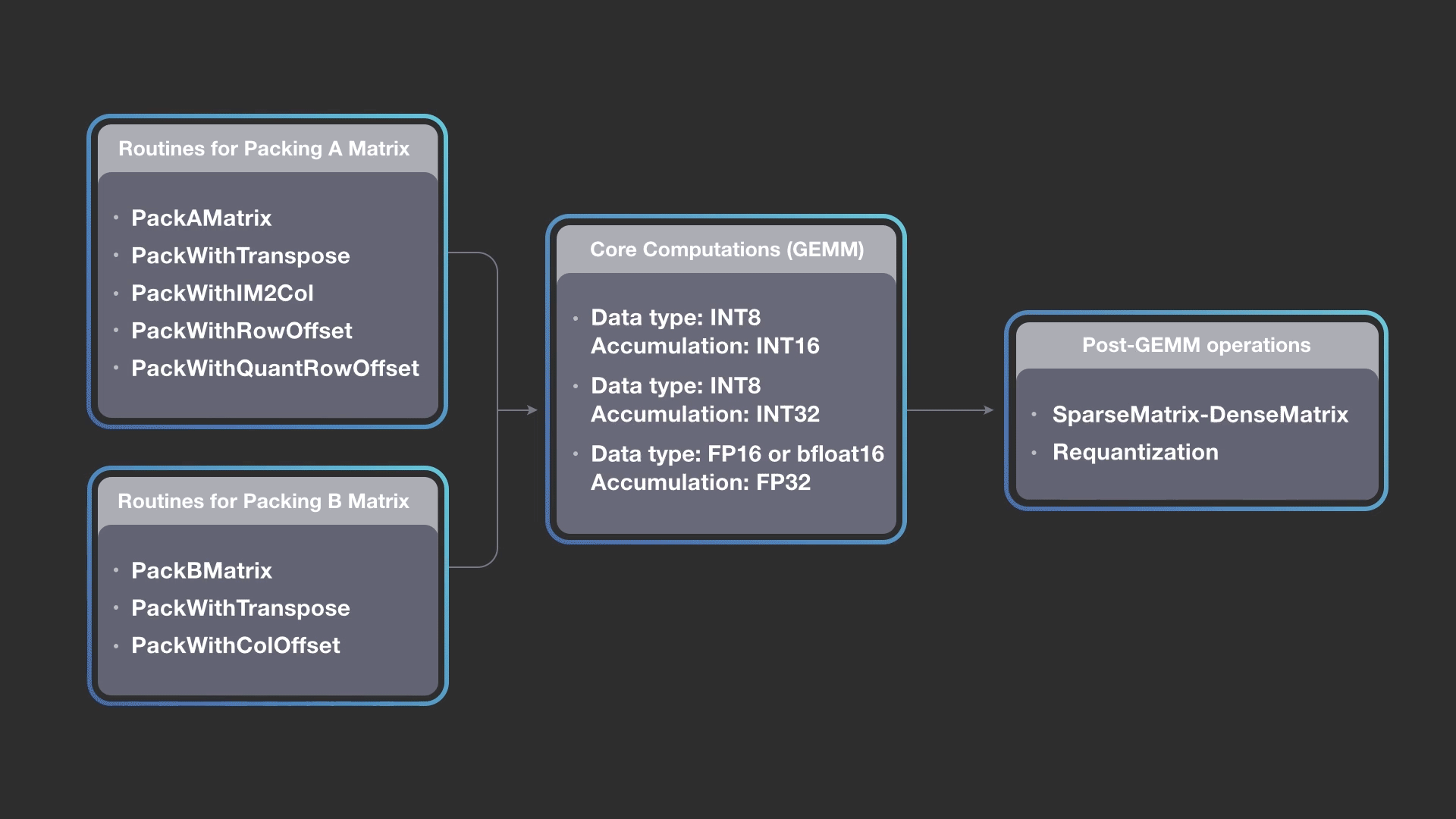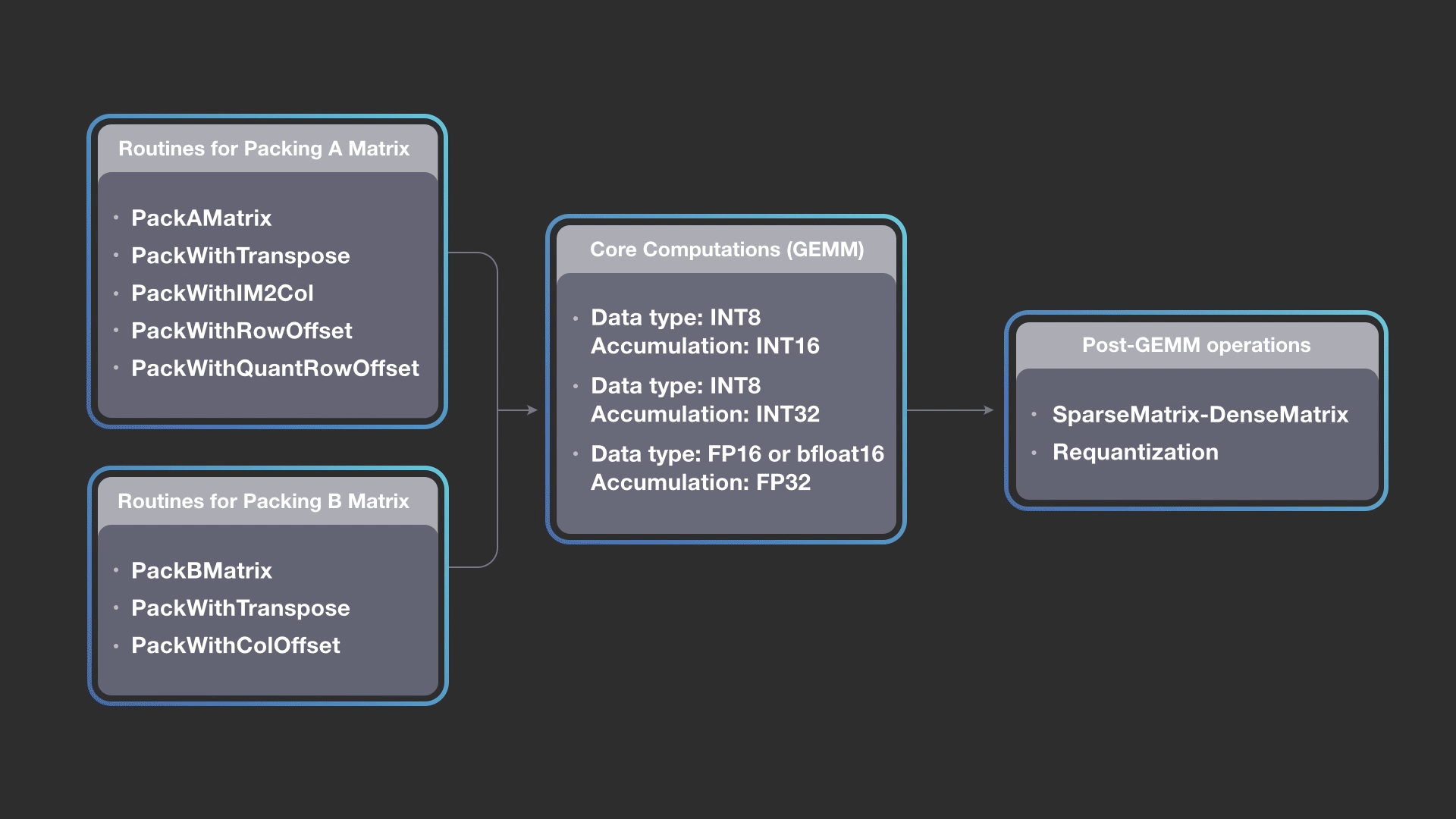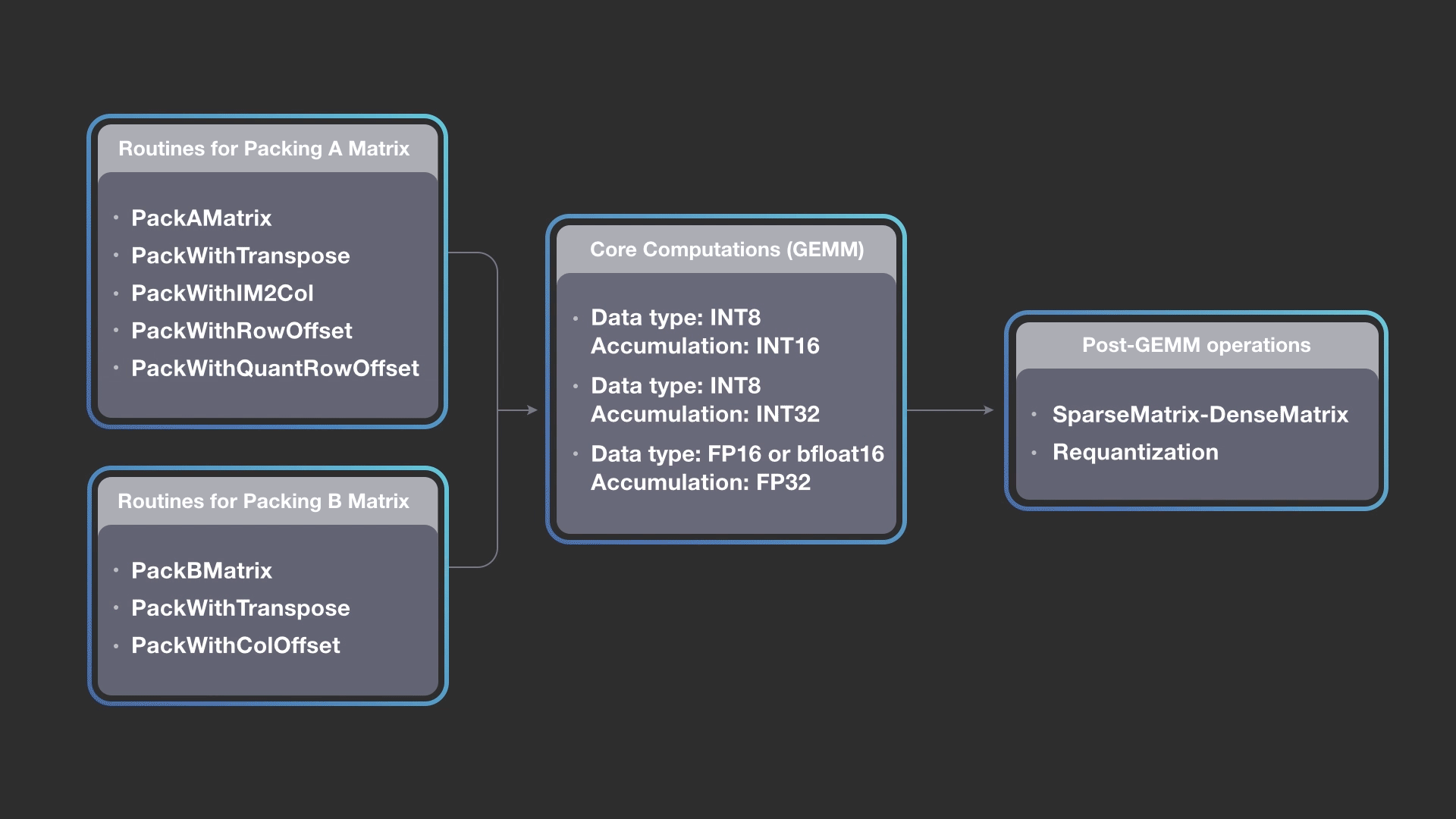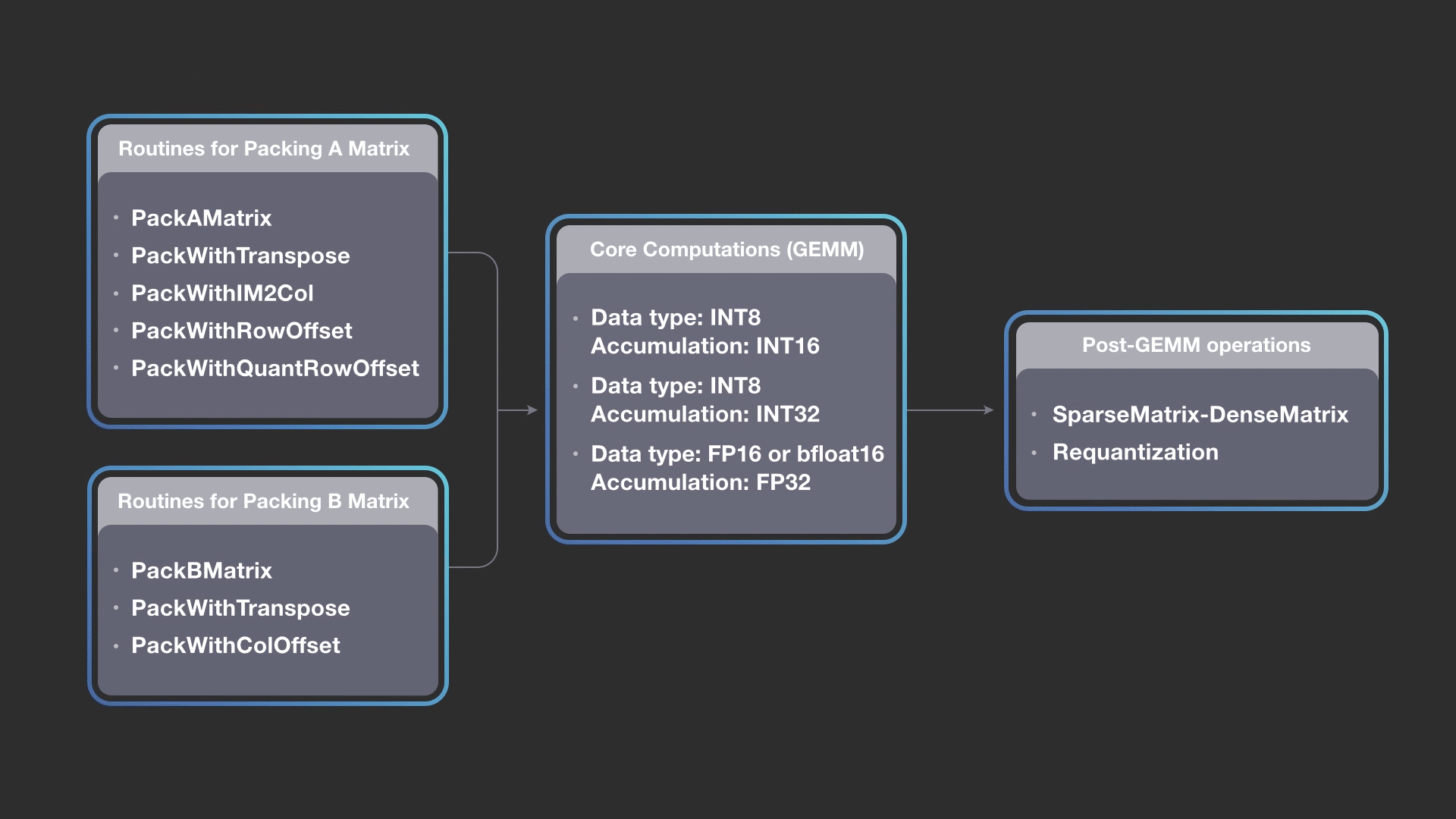
The diagram above shows how we can combine different packing methods for A and B matrices while keeping the core computations the same, and then construct a pipeline of output operations. FBGEMM implementation allows you to construct a pipeline by picking any packing routine for A, any packing routine for B, any of the core kernels (accumulation into INT16, INT32, or FP32), and any combination of post-GEMM operations. The design is extensible, and newer packing or post operations can be added into the FBGEMM library as needed. The gemmlowp library also allows composing the core kernel with a post-GEMM operation called output pipeline, but FBGEMM extends it to input packing.
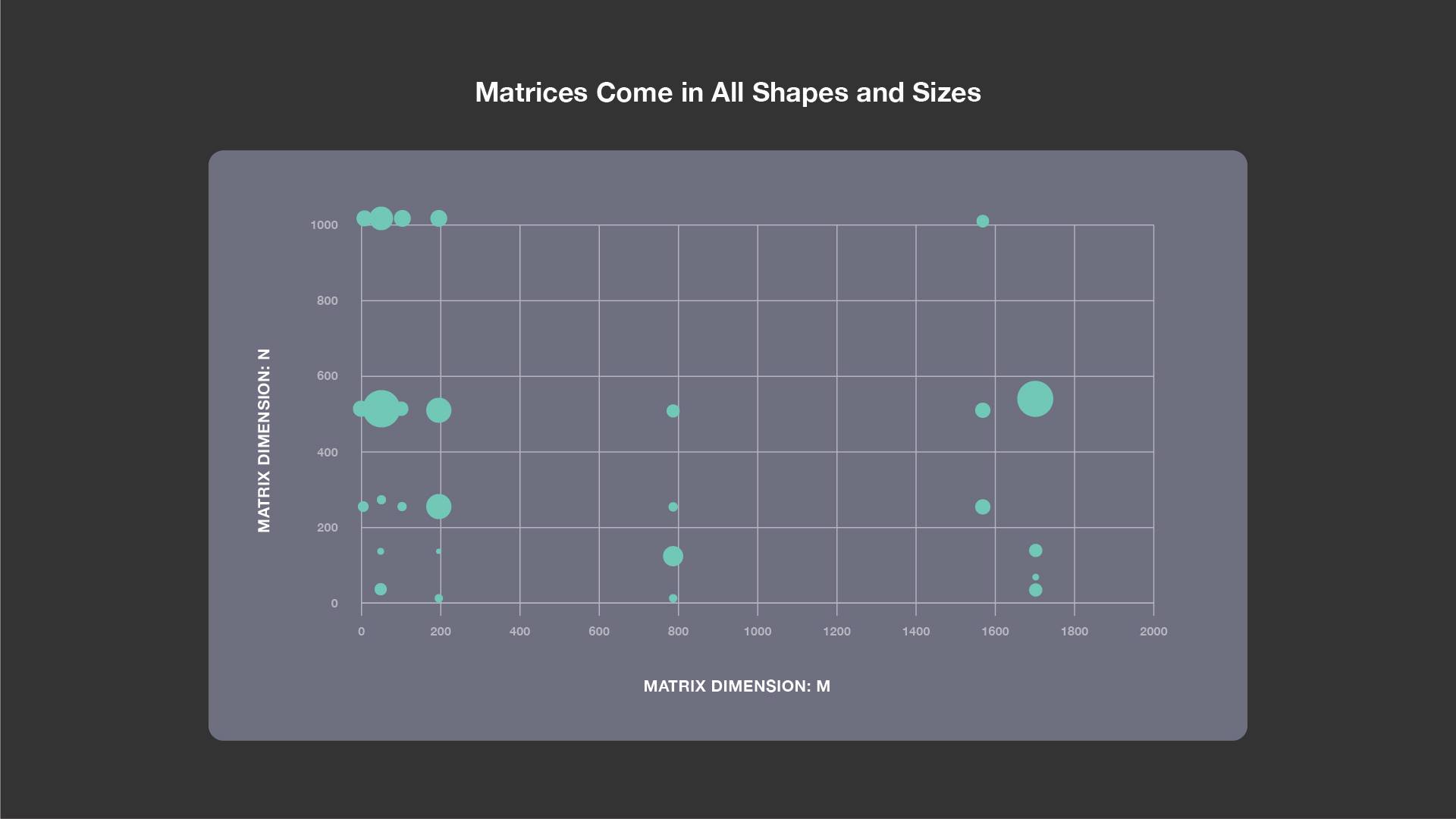
Typically, GEMM libraries from HPC domains are optimized for large matrices that are square or almost square. For matrix multiplications in networks such as Faster-RCNN — which is used in Rosetta, Resnet50, Speech, and NMT — the most commonly occurring shapes are shown in the figure below.
Each bubble represents typical M, N, and K dimensions for matrix-matrix multiplications. The size of the bubble is proportional to the K value. As is clear from the figure, matrices come in all shapes and sizes. M is sometimes very small, and at other times N is very small. We need efficient implementations for all of these cases.
With inner kernels, FBGEMM takes a “one size doesn’t fit all” approach, so the implementation dynamically generates efficient matrix-shape specific vectorized code. For example, if we see at runtime that M is 1, we query whether or not an efficient kernel exists for M = 1 and use that if so. If not, we generate that kernel, store it in the kernel cache, and use it. We need to carefully craft only a few kernels, then map other matrix dimensions to them.
Overall, the optimized loop structure for our implementation looks as follows:
Loop1 for ic = 0 to M-1 in steps of MCB
Loop2 for kc = 0 to K-1 in steps of KCB
//Pack MCBxKCB block of A
Loop3 for jc = 0 to N-1 in steps of NCB
//--------------------Inner Kernel------------
//Dynamically generated inner kernel
//Loop4 and Loop5 are in assembly
FBGEMM is a C++ library, and the following code listing shows the GEMM interface that it exposes. The flexible interface is implemented with the help of C++ templates.
template<
typename packingAMatrix,
typename packingBMatrix,
typename cT,
typename processOutputType>
void fbgemmPacked(
PackMatrix<packingAMatrix,
typename packingAMatrix::inpType,
typename packingAMatrix::accType>& packA,
PackMatrix<packingBMatrix,
typename packingBMatrix::inpType,
typename packingBMatrix::accType>& packB,
cT* C,
void* C_buffer,
std::int32_t ldc,
const processOutputType& outProcess,
int thread_id,
int num_threads);
The interface is specifically designed to support optimized quantized inference and fusion of post-GEMM operations. The template parameters packA and packB provide packing routines for the current block. Because FBGEMM is targeted toward inference, we assumed that the B matrix is already packed (i.e., the packB.pack function is never called). The next three arguments are related to the C matrix. C is the pointer to the C matrix itself. C_buffer is the pointer to a preallocated buffer memory that is used to store intermediate 32-bit integers or FP32 values. And ldc is the standard leading dimensions of the C matrix. outProcess is a template argument that can be a C++ functor implementing a pipeline of output processing elements. It is called after a block of C matrix is computed in the C matrix to take advantage of cache locality. The final two parameters are related to parallelization. Internally, FBGEMM is intentionally designed not to create any threads. Usually, such a library is intended to be used as a backend by deep learning frameworks, such as PyTorch and Caffe2, that create and manage their own threads. Overall, this interface allows use of different packing methods and the construction of a pipeline of post-GEMM operations on the currently computed block of output matrix.
Because depthwise convolution is sufficiently different from GEMM, we also include a specialized kernel for it in FBGEMM. We believe most of the important use cases found in our data centers (including convolutions) can be efficiently implemented using our approach of composing various input-packing and output-processing operations. As with QNNPACK, our depthwise convolution kernel vectorizes over channels. But it takes advantage of size constraints for code not being as strict as mobile platforms, allowing us to do more aggressive unrolling and inlining with template specializations. Compared with QNNPACK — which needs to prepare various requantization options, including the ones purely using fixed-point operations in case the target platform lacks good floating-point supports — FBGEMM uses FP32 operations when scaling INT32 intermediate GEMM output to INT8 during requantization.
A sample end-to-end FBGEMM pipeline
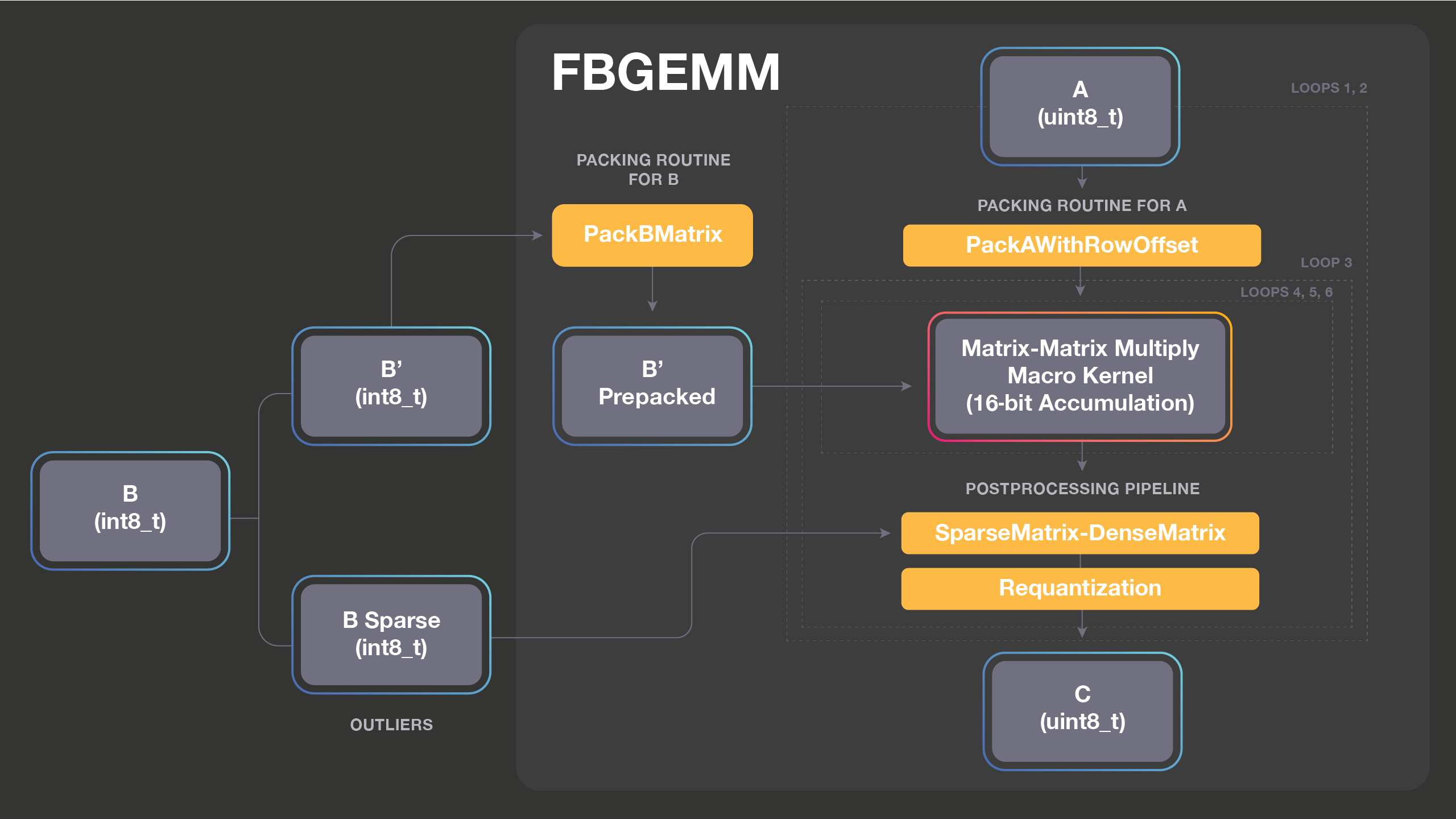
The FBGEMM interface allows for flexible composition with various output processing schemes, which is illustrated by how we perform 16-bit accumulation (depicted by the figure below). FBGEMM supports INT8 matrix multiplication with INT16 accumulation to get better performance for compute-bound cases. INT8 FMA with accumulation into INT16 is performed with a combination of vpmaddubsw and vpaddsw vector instructions. With INT8, we work on 4x more elements in comparison with FP32 per vector instruction, but we use two vector instructions for each vector FMA. Therefore, theoretical peak for accumulating into 16 bits is 2x that of FP32. INT16 accumulation, however, usually leads to frequent overflow/saturation, which we avoid by using outlier-aware quantization. That is, we split matrix B into B = B’ + B_sparse, where B’ has numbers only with small magnitude, and big numbers are separated as B_sparse. We denote the matrix with outlier numbers as B_sparse because B typically has only a few big numbers so B_sparse is usually very sparse. After the splitting, A * B can be computed as A * B’ + A * B_sparse, where we can safely use INT16 accumulation for A * B’ because B’ only contains small numbers. The majority of computation will happen in A * B’ given the sparsity of B_sparse.
The splitting of B, packing of B’, and converting B_sparse in an efficient sparse matrix format (we use compressed sparse column) needs to be done only once as a preprocessing step because B is constant during inference. FBGEMM computes dense matrix times sparse matrix multiplication (i.e., A * B’) as a part of the postprocessing pipeline. Sparse matrix computation is usually a memory-bandwidth-bound operation, so it is important to fuse it with the main computation. Instead of computing A * B’ and A * B_sparse separately, they are fused so a part of A * B_sparse can be computed when packed A and partial result of C is cache-resident.
Performance impact and results
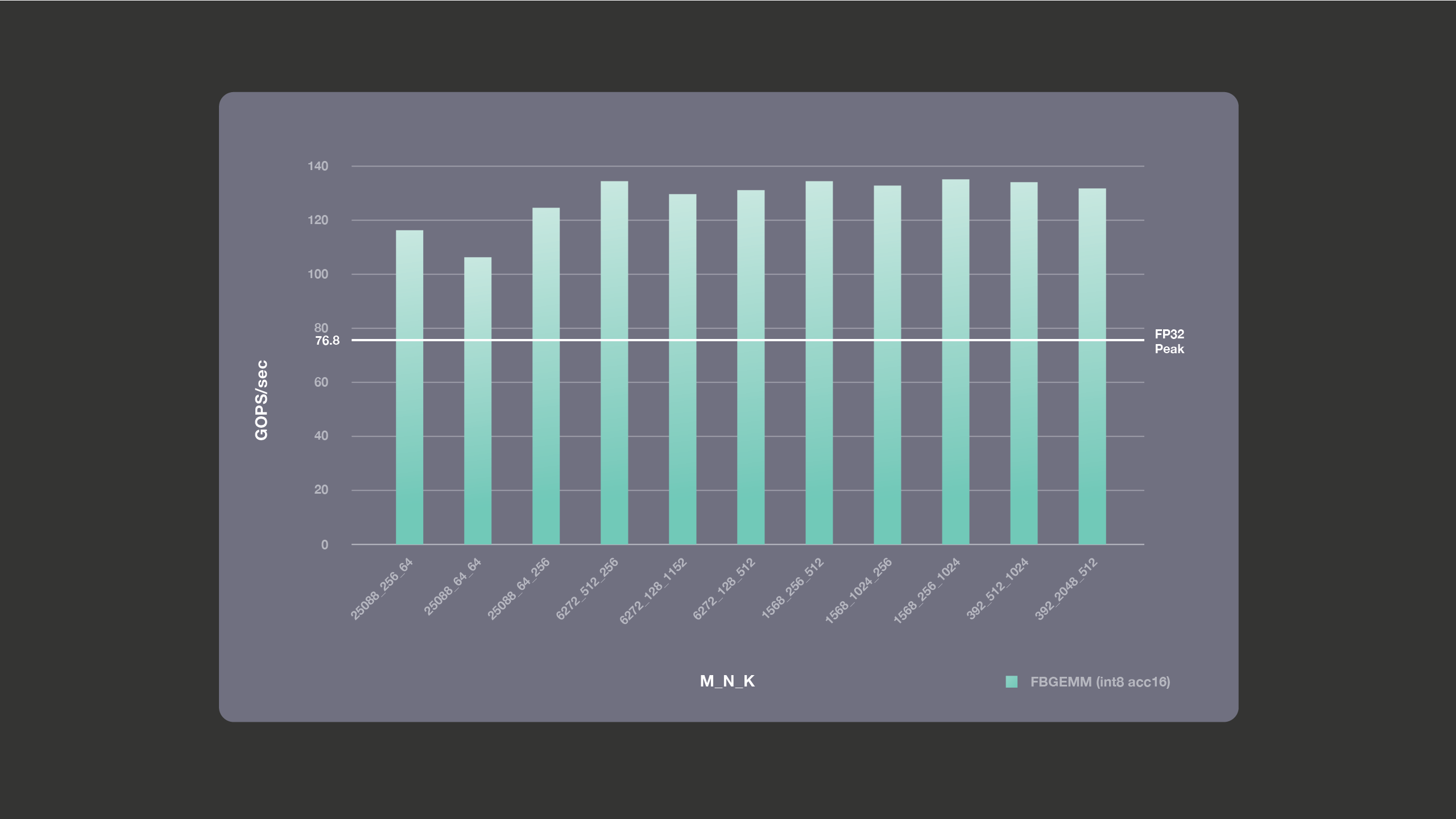
We ran performance benchmarking for the FBGEMM library on Intel(R) Xeon(R) CPU E5-2680 v4 using a single thread on a single core. We used a Broadwell machine with a base frequency of 2.4 GHz, with turbo mode disabled to get reliable run-to-run results. The following graph shows the FP32 theoretical peak number against the actual performance we get for INT8 GEMMs with accumulation into 16 bits. As mentioned earlier, theoretical single-core peak for accumulation into 16 bits for this Broadwell machine is 2x the FP32 peak, i.e., 153.6 giga operations per second (GOPS). Accumulation into 16 bits is used for the cases that are compute-bound, as these are the cases in which we get the most performance benefits. For the bandwith-bound cases, accumulation into 16 bits does not buy us any better performance, but accumulation into 16 bits may overflow unless we use outlier-aware quantization; hence, we avoid using accumulation into 16 bits for bandwidth-bound cases.
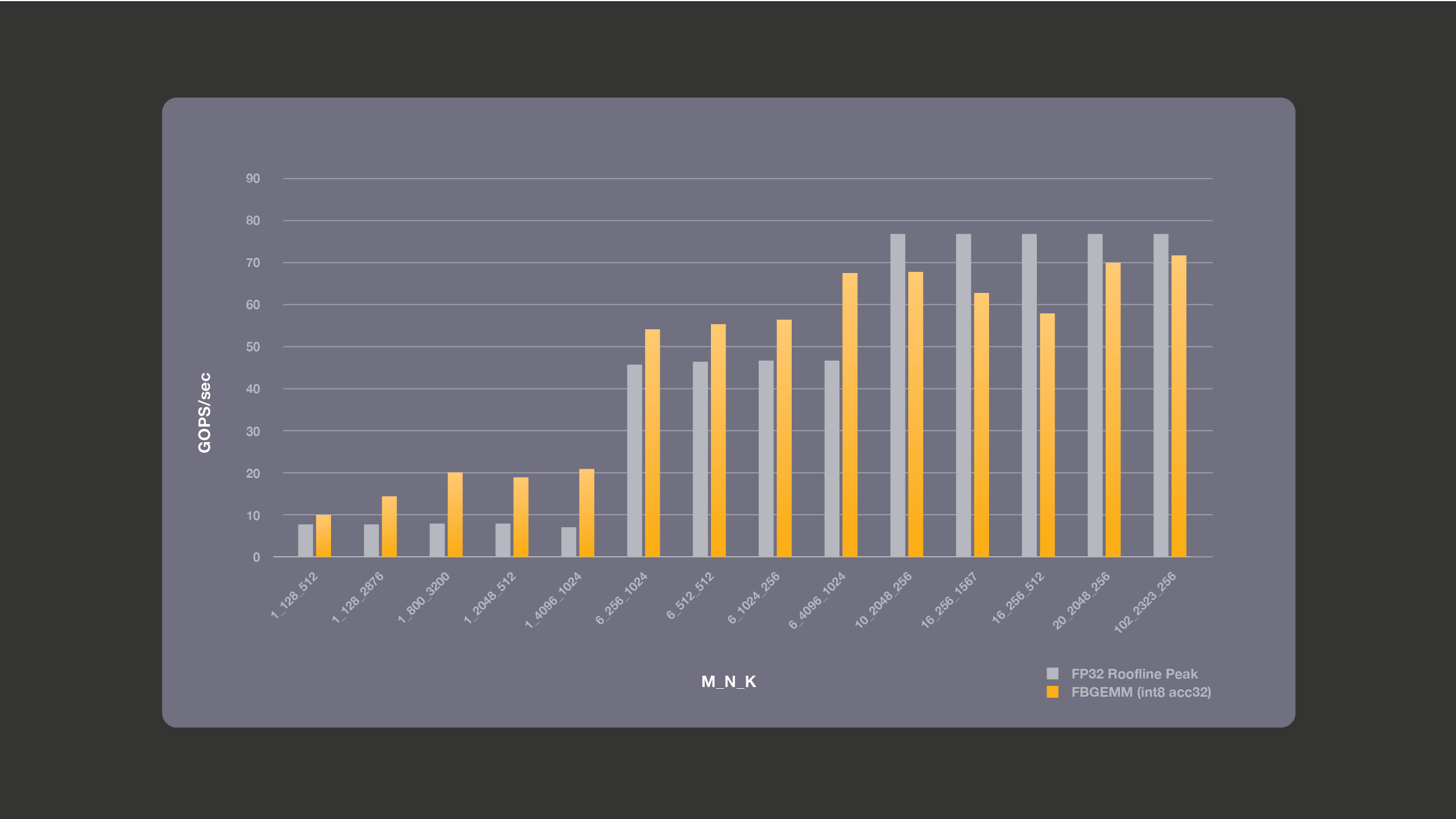
The following graph shows performance for the bandwidth-bound cases, where we perform accumulation into 32 bits. INT8 FMA with INT32 accumulation is performed with a combination of vpbroadcastd, vpmaddubsw, vpmaddwd, and vpaddd vector instructions. Since 4 instructions are used for INT8 FMA , the theoretical compute peak for INT8 is not better than FP32 even though each element size is 4x smaller. The figure also shows the roofline peak for the same machine. Overall, the Broadwell machine has a theoretical peak bandwidth of 76.8 Gigabyte/sec for all cores. We measured a stream triad bandwidth of 15.6 GB/sec per core and use this number to calculate roofline peak. FP32 roofline peak numbers are the best theoretically possible numbers and in practice the achieved performance is lesser than these roofline numbers. We compare INT8 performance against these theoretically best numbers for FP32. As shown in the graph below, accumulation into 32 bits is most beneficial for the small batches. Matrix dimension M is the batch dimension. We are able to achieve better-than-FP32 theoretical roofline performance, because of the benefits of using less bandwidth, by working with lower precision data.
What lies ahead
Quantized inference is already proving useful on the current generation of server hardware. Careful implementation of quantization has shown us encouraging results on language translation models, recommendation systems, and models for text understanding in images and videos. But we can continue to build on our work with FBGEMM. There are a variety of other models in use across Facebook in which quantized inference is not yet implemented, and FBGEMM combined with a deep learning framework has the potential to improve efficiency there as well. Certain newer models, such as ResNeXt-101 and ResNext3D, are more accurate but are so compute-heavy that deploying them at scale is very resource-intensive without improved efficiency. We hope that FBGEMM will help fill the necessary efficiency gap for deployment.
As the deep learning models in computer vision grow wider and deeper in search of better accuracy, the use of groupwise convolution and depthwise — a special case of groupwise — convolution is increasing. When the number of groups is large, however, groupwise convolution is inefficient when performed with im2col followed by the GEMM method. We already have a specialized implementation for depthwise convolutions, but we intend to add direct groupwise convolution to FBGEMM as well. The most-frequently-used Caffe2 operators are already implemented using FBGEMM, and a direct integration with PyTorch is planned. We are also planning to add more features to further improve efficiency, such as merging depthwise convolution with 1×1 convolution and improving performance-debugging support.
We hope open-sourcing FBGEMM will allow other engineers to take advantage of this high-performance kernel library, and we welcome contributions and suggestions from the wider community. The HPC community has long provided the standard interface for GEMM, and with FBGEMM, we show that combining certain operations with input and output packing is more efficient. We hope future GEMM interfaces from the HPC community will find inspiration in these ideas.
We’d like to acknowledge the contributions to this project from the FBGEMM team, along with the AI developer platform team and our AI system co-design group.









